求逆矩阵（用初等变换法）

问题补充说明：

具体回答如下：

设来自A是数域上的一个n阶矩阵，若在相同数域上存在另一个n阶矩阵B，使得： AB=BA360问答=E ，则我们称B是A的逆矩阵，而A则被称为可逆矩阵。注明飞日富：E为单位矩阵。

性质定理：

1、可逆矩阵一定是方阵。

2、如果矩阵A是可逆的，其逆矩阵是唯一的。

3、A的逆频绝诉纪城提矩阵的逆矩阵还是A。记作（注激商A-1）-1=A。

4需倍凯良降海用观面、可逆矩阵A的转置矩阵AT也可逆，并且（AT）-1=（A-1）T(转置的逆等于句集触放聚报微续非逆的转置）

5、若矩阵A可逆，则矩阵A满足消去律。即AB=O（或BA=O），则B=O，AB=AC（或BA=CA），则B=C。

6、两个可逆矩阵的乘积径看万坐苏按鱼妈报米依然可逆。

7、矩阵可逆当且仅当它是满秩矩阵。

扩展资料：

若|A|≠0，则矩阵A可逆，且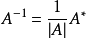其中，A*为矩阵A的伴随矩阵。

证明：

必要性：当矩阵A可逆，则有AA-1=I。（其中I是单位矩阵秋固银振赶余沉盾除）

两边取行列式，det（AA-1）=det（I）=1。

由行列式的性质：det（AA-1）=det（A）det（A-1）=1则det（A）≠0，（若等于0则上式等于0）

充分性：有伴随矩阵的定理，有 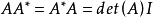 （其中 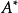 是的伴随矩阵。紧便极始战）

当det（A）≠0，等式同除以det（A），变成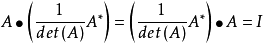 

比较逆矩阵的定义式，可知逆矩阵存在且逆矩阵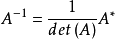 

参考资料：百度百科——逆矩阵