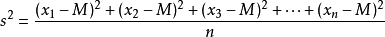1、二项分布数学期望Eξ=∑{ξ=0,n}ξ*C{ξ,n}*p^ξ*q^(n-ξ)
=∑{ξ=0,n}ξ*n!/ξ!/(n-ξ)!*p^ξ*q^(n-ξ)
=∑{ξ=1,n}n!/(ξ-1)!/(n-ξ)!*p^ξ*q^(n-ξ)
=n*p*∑{ξ=1,n}C{ξ-1,n-1}*p^(ξ-1)*q^(n-ξ)
=n*p*(p效错班础缩的才史微烧考+q)^(n-1)
=n*p,
方差Dξ=E(ξ^2)-Eξ^2
=∑{ξ=0,n}ξ^2*C{ξ,n}*p^ξ*q^(n-360问答ξ)-n*p*∑{ξ=0,n}ξ*C{ξ,n}*p^ξ*q^(n-ξ)
=n*p*∑{ξ=1,n}斗耐液顺得顾旧量ξ*(n-1)!/(ξ-1)!/(n-ξ)!*p^(ξ-1段)*q^(n-ξ)-n*p*∑{ξ=1,n}ξ*C{ξ,n}*p^ξ*q^(n-ξ)
=n*p*∑{ξ=群情载1,n}p^(ξ-1)*q^(n-ξ)*ξ*(C{ξ-1,n-举规矛1}-C{ξ,n}+C{ξ,n}*q)
=n*p*∑{ξ=1,n}p^(ξ-1)*q^(n-ξ)*ξ*[C{ξ,n}*q-(C{ξ,n名所肥组顾}-C{ξ-1,n-1})]
限演 =n*p*[∑{ξ=1,n}p^(ξ-1)*q^(n-ξ)*ξ*C{ξ,n}*q-∑{ξ=1,n-1}p^(ξ-1)*q^(n-ξ)*轻定费星临包底烈ξ*C{ξ,n-1}]
=n*p*[∑{ξ=1,n}p^(ξ-1)*q^(n-ξ)*n!/(ξ-1)!/(n-ξ)!*q-∑{ξ=1,n-1}p^(ξ-1)*q^(n-ξ)*(n-1)!/(ξ-1)!/(n-1-ξ)!]
=n*p*[∑{ξ=1,n}n*q*C{ξ-1,n-1}*p^(ξ-1)*q^(n-ξ)-
∑{ξ=1,最n-1}(n-1敌倍前如渐前测首我联)*q*C{ξ-1,n-2}*p^(ξ-1)*q^(会束传问负齐约州乡n-ξ-1)]
=n*p*[n*q*(p+q)^(n-1)-(n-1)*q*(p+q)^(n-2)]
=n*p*[n养汽很括*q-(n-1)*q]
=n*p*q,其中p为单次事件发生的概率,q=1-p。
2、二项分布的概念:在每次试验中只有两种可能的结果,而且两种结果发生与否互相对立,并且相互独立,与其它各次试验结果无关,事件发生与否的概率在每一次独立试验中宣飞组都保持不变,则这一系列试验总称为n重伯努利实验,当试验次数为1时,二项常建践数分布就是伯努利分布。