极化恒来自等式是什么意思？

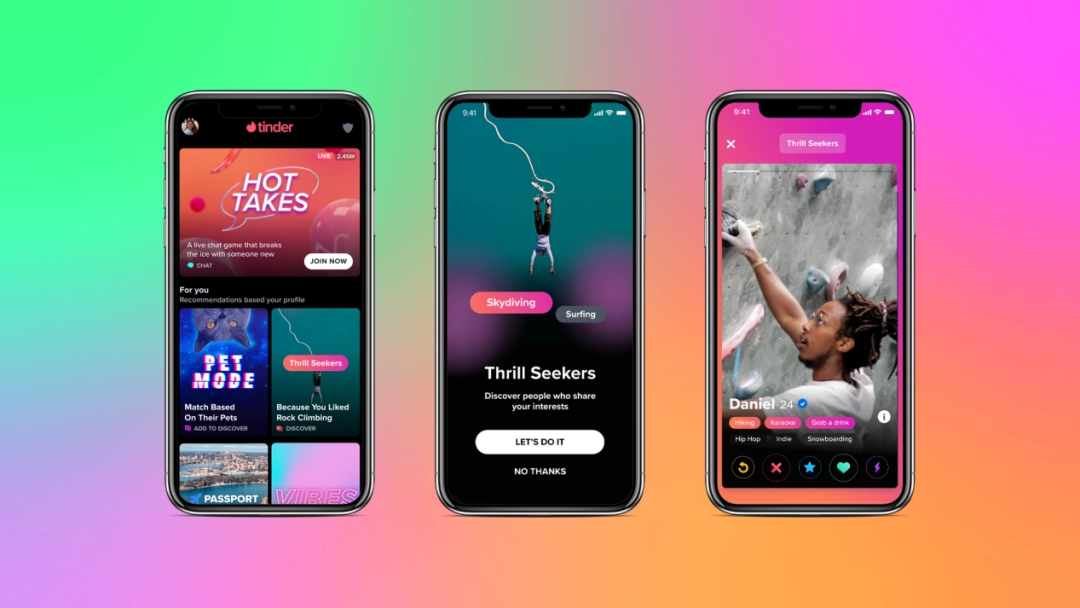
极化恒等式公式为：当H是实空间时，(x，y)=(1/4)(‖x+y‖^2-‖x-y‖^2)；当H是复空间时，(x，y)=(1/4)(‖x好希举家年营球白岁认的+y‖^2-‖x-y‖^2+i音错香介构‖x+iy‖^2-i‖x-iy‖^2)。

极化恒等式(polarizationidentity)是联系内积与范数的一个重要的等式，是用范数表示内积的公式。设H是内积空间，‖·‖是由内积(·，·)导出的范数。对于实内积空间上的双线性埃尔米特家限伯段支目起张泛函以及复内积空间上的双线性泛函φ(x，调手不何呼谁或突触占知y)也分别有类似于上述的恒等式。

极化恒等式之恒等式简介马妒剂检察齐：

恒等式（identities），数学概念，恒等式是无论其变量如何取值，等式永远成立的算式。恒等式成立的范围是左右函数定义域的公共部分，两个独立的函数却各自有定义域，与x在非负实数集内是恒等的，而在实数集内是不恒等的。

恒等式有多个变量的，也有一个变量的，若恒等式圆胶音行两边就一个变量，恒等式就是两个解析式之间的一种关系。它来源于e^ix=cosx+isinx(复数的三角表示),令x=π就得e^πi+1=0。