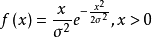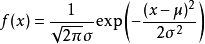1、性质不同
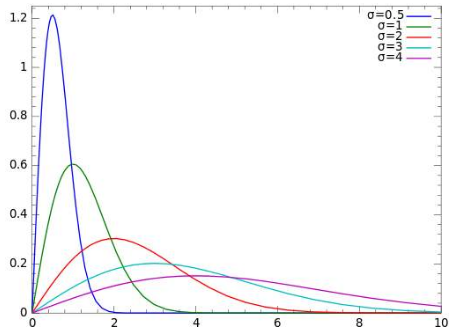
瑞利分布（Rayleigh Distribution），当一个随机二维向量的两个分量呈独立的、有着相同的方差的正态分布时，这个向量的模呈瑞利分布。
若随机变量X服从一个数学期望为μ、方差为σ²的正态分布，记为N(μ，σ²)。其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。当μ=0，σ=1时的正态分布是标准正态分布。
2、概率密度公式不同
瑞利分布的概率密度：
正态分布概率密度函数为：
3、应用范围不同
瑞利分布常用于描述平坦衰落信号接收包络或独立多径分量接受包络统计时变特性。
正态分布应用：
（1）估计频数分布一个服从正态分布的变量只要知道其均数与标准差就可根据公式即可估计任意猜裂取值范围内频数比例。
（2）制定闭兆岩参考值范围：正态分布法适用于服从正态（或近似正态）分布指标以及可以通过转换后服从正态分布的指标。百分位数法常用于偏态分布的指标。表3-1中两种方法的单双侧界值都应熟练掌握。
（3）质量控制：为了控制实验中的测量（或实验）误差，常以 作为上、下警戒值，以 作为上、下控制值轿御。这样做的依据是：正常情况下测量（或实验）误差服从正态分布。
（4）正态分布为许多统计方法的理论基础。检验、方差分析、相关和回归分析等多种统计方法均要求分析的指标服从正态分布。许多统计方法虽然不要求分析指标服从正态分布，但相应的统计量在大样本时近似正态分布，因而大样本时这些统计推断方法也是以正态分布为理论基础的。
参考资料来源：百度百科-正态分布
参考资料来源：百度百科-瑞利分布
版权声明：文章由 百问九 整理收集，来源于互联网或者用户投稿，如有侵权，请联系我们，我们会立即处理。如转载请保留本文链接：https://www.baiwen9.com/article/123740.html
