三角形中位线定理的定理

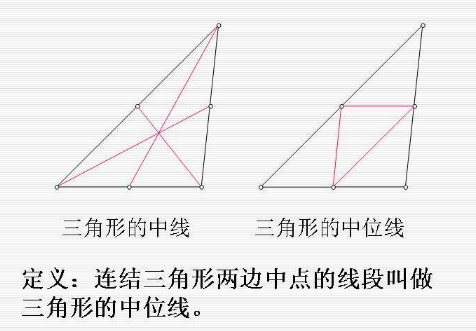
三角形的中位线平行于第三边（不与中位线接触），并且等于第三边的一半。

证明：

已知△ABC中，D，E分别是AB，AC两边中点。

求证DE平行兆态于BC且等闹猜尺于BC/2

方法一：过C作AB的平行线交DE的延长线于G点。

∵CG∥AD

∴∠A=∠ACG

∵∠AED=∠CEG、AE=CE、∠A=∠ACG（用大括号）

∴△ADE≌△CGE （A.S.A)

∴AD=CG(全等三角形对应边相等)

∵D为AB中点

∴AD=BD

∴BD=CG

又∵BD∥CG

∴BCGD是平行四边形（一组对边平行且相液高等的四边形是平行四边形）

∴DG∥BC且DG=BC

∴DE=DG/2=BC/2

∴三角形的中位线定理成立。

扩展资料：

逆定理

在三角形内，与三角形的两边相交，平行且等于三角形第三边一半的线段是三角形的中位线 [2]  。

如图DE//BC，DE=BC/2，则D是AB的中点，E是AC的中点。

证明：∵DE∥BC

∴△ADE∽△ABC

∴AD:AB=AE:AC=DE:BC=1:2

∴AD=AB/2，AE=AC/2，即D是AB中点，E是AC中点。