摆线的方程是什么？

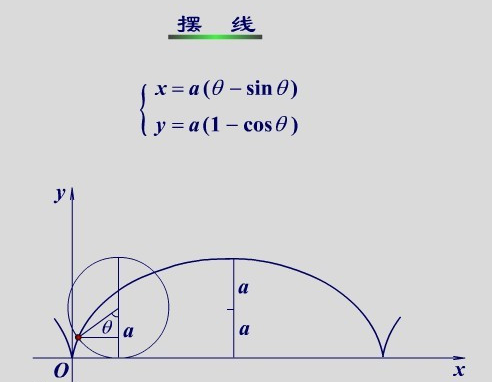
x=r*(t-sint)； y=r*(1-cost)r为圆的半径， t是圆的半径所经过的弧度（滚动角），当t由0变到2π时，动点就画出了摆线的一支，称为一拱。

由摆线x=a（t - sint），y=a（1 -cost）的一拱（0≤t≤2π） 与横轴所围图形的面积为3π*a^2。

解：根据定积分求面积公式，以x为积分变量，可得摆线的一拱与横轴所围图形的面积S为，S=∫|y| dx=∫a（1 -cost）d（a（t - sint））=∫a^2（1 -cost）^2dt

扩展资料

摆线最早出现可见于公元 1501 年出版的 C·鲍威尔的一本书中．但在 17 世 纪，大批卓越的数学家（如伽利略，帕斯卡，托里拆利，笛卡儿，费尔马， 伍任，瓦里斯，惠更斯，约翰·伯努利，莱布尼兹，牛顿等等）热心于研究这一曲线的性质。

17 世纪是人们对数学力学和数学运动学爱好的年代，这能解释人们为什么对摆线怀有强烈的兴趣。在这一时期，伴随着许多发现，也出现了众多有关发现权的争议，剽窃的指责，以及抹煞他人工作的现象。这样，作为一种结果，摆线被贴上了引发争议的“金苹果”和“几何的海伦” 的标签。