棱台的特征

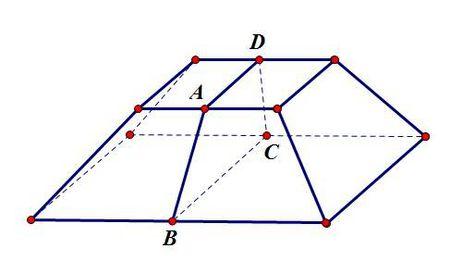
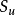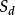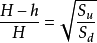1、正棱台的侧棱相等，侧面是全等的等腰梯形。各等腰梯形的高相等，它叫做正棱台的斜高；

2、正棱台的两底面以及平行于底面的截面是相似正多边形；

3、正棱台的两底面中心连线、相应的边心距和斜高组成一个直角梯形；两底面中心连线、侧棱和两底面相应的半径也组成一个直角梯形。

4、棱台各棱的反向延长线交于一点。

5、棱台的结构特征：用一个平行于棱锥底面的平面去截棱锥,底面与截面之间的部分是棱台。

6、下底面和上底面：原棱锥的底面和截面 分别叫做棱台的下底面和上底面。

7、侧面：原棱锥的侧面也叫做棱台的侧面（截后剩余部分）。

8、侧棱：原棱锥的侧棱也叫棱台的侧棱（截后剩余部分）。

9、顶点：上底面和侧面，下底面和侧面的公共点叫做棱台的顶点。

棱台的表示：用表示底面的各顶点的字母表示。  如：棱台ABCD-A’B’C’D’。底面是三角形，四边形，五边形----的棱台分别叫三棱台，四棱台，五棱台。

扩展资料

棱台的体积取决于两底面之间的距离（棱台的高），以烂大及原来棱锥的体积。

设h为棱台的高，  ，  为棱台的上下底面积，V为棱台的体积。

由于棱台是由一个平面截去棱锥的一部分（也就是和原来棱锥相似的一个小棱锥）得到，所以计困拿算体积的时候，可以先算出原来棱锥的体积，再减去和它相似的小棱锥的体积。

棱锥被平行于底面的平面所截时，截面的面积与底面面积的比，等于小棱锥和原棱汪历搭锥的高的比的平方。假设原棱锥的高是H，那幺小棱锥的高是H-h。也就是说：

所以：

棱台的体积等于原棱锥体积减去小棱锥的体积：

参考资料来源：百度百科-棱台