朋友,这个三角问题的范围问题,用语言不太好表达!我下面会用一些我画的图和相关文字说明一下,希望对你有帮助!
首先画出本题对应的一般图形!
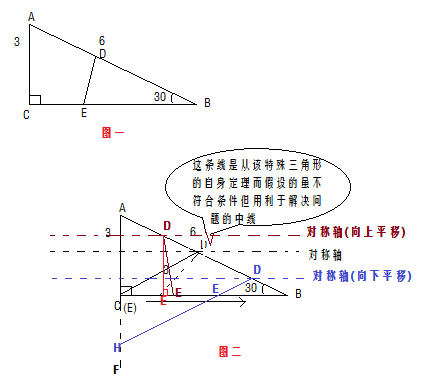
如下:
由三角关系:因为AB=6,又<ABC=30°,所以AC=3!
本题需要我们在几何关系上找出突破口!恰好本题给我们的是一个很特殊的直角三角形,即包含30°的三角形!所以我们应该意识到此题的意图,为什么不用腊老派其他的三角形,而恰恰是这样的特殊直角三角形?呵呵···是因为这样的三角形包含了一个很重要的性质!就是这样一条定理:“30°角所对的直角边长度是斜边的一半,且斜边上的中线长度也是斜边的一半!”
在此,题目中说点E是BC边上一点(不与点B和C点重合),括号里强调了不与点B和点C重合!
下面我们假设E与C点重合,且D是AB的中点,那么此时符合了题意后面的要求,即DA=DE,但这是为了解决问题假设E与C点重合的,实际不符合!即AD不会等于3,下面接着这种假设前进,希望不要烦啊!
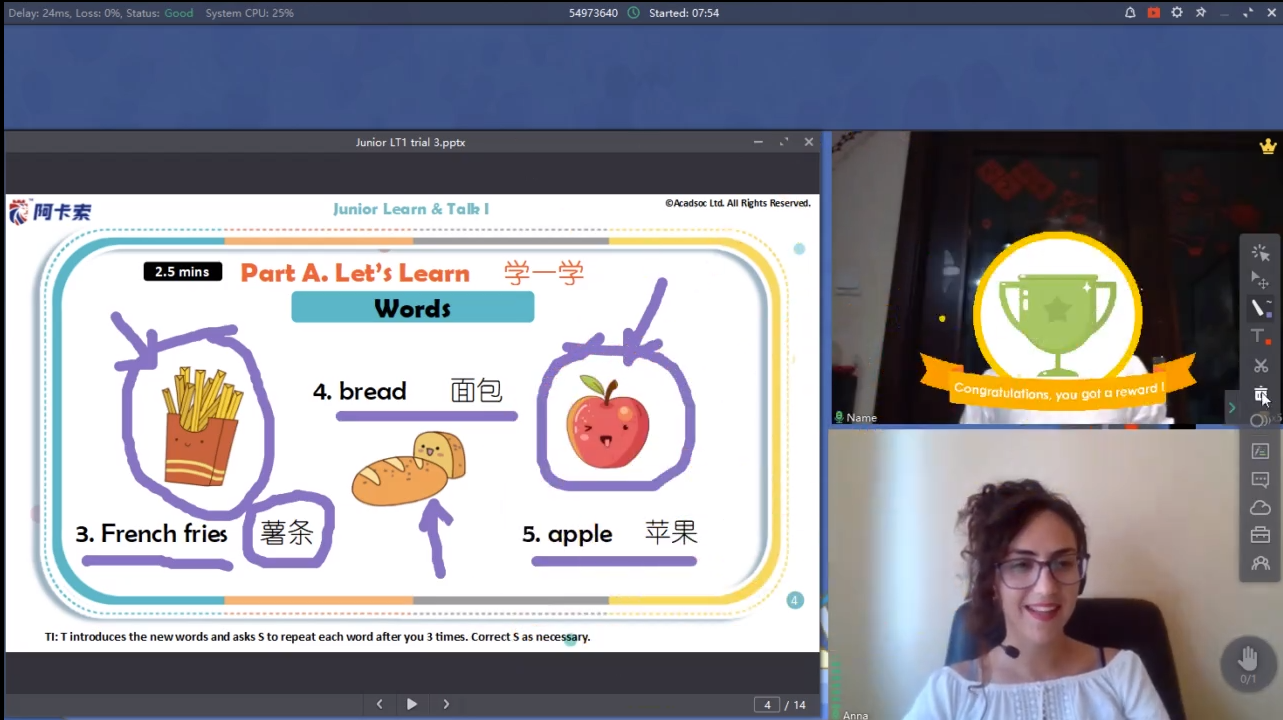
接着对着下幅图理解:
首先来看若D为中点,而为了符合E不与C点重合,我们将E点从C点向B点移动,很显然,经移动观察后,到最后只有B点符合AD=DE,但是E要求也不与B重合,所以可以知道D为中点时不能出现AD=DE的情况!于是我们需要把D点在中点左右移动看看!我在图上画了一条假设线的一个对称轴,如果我们将此直线向下平移,其实也就是D点向下移动(注意此时相应的对称轴也会向下移动),我们在中点一下任取一点D,此时我们用对称关系来找在BC上符合条件的点E,根据思路画出对称轴后,发现AD=DH,(H是作对称后在AC延长长线上的交点),而E点对应的DE<DH,即使将E点向右移动,依然是DE<DH,也就是DE<AD!所以肯定当D点在斜边中点一下,找不到题目要求的关系范围!
下面看D点在中点上面!当D向上移动时,AD长度减小,而DE长度增加,所以中间必有含卖一个平衡点,使得AD=DE!当D点再向上移动时,则再轮贺也找不到这种关系!我们可以想象,为了尽可能满足条件,我们可以知道一个临界状态:就是当D点满足DE垂直BC且DE=AD时为D的临界点!
为什么这么说呢?因为D点向上移动,则D点距离BC越来越远,其中最小距离为D点到BC的垂直距离!而AD长度越来越小,我们在找寻等价关系时,只能将D距离BC最小长度的直线和AD比较才可以!当D点到BC直线的距离比AD长度还大时,则意味着后来再向上移动也不会有符合题目的点存在!根据关系,设临界时AD=X,则BD=6-X,又DE垂直BC且<ABC=30°,则DE=(6-X)/2,列出等价关系为X=(6-X)/2 解得X=2!最后得出AD的范围为 2≤AD<3!
朋友,希望对你有帮助!我尽我所能了!说得好,记得给我多加分哦!以后还会帮你!