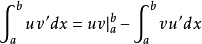分部积分法怎么理解分部积分法不好理解呢,能介绍下么

一、分部积分法的定义：

设u=u(x),v=v（x)均在区间[a,b]上可导，且u′，v′∈R（[a,b]),则有分部积分公式：

二、分部积分法的理解：

1、设函数和u，v具有连续导数，则d(uv)=udv+vdu。移项得到udv=d(uv)-vdu；

2、两边积分，得分部积分公式∫udv=uv-∫vdu。

3、如果积分∫vdu易于求出，则左端积分式随之得到。

4、分部李则积分公式运用成败的关键是恰当地选择u，v。

5、一般来说，u,v 选取的原则是：积分容易者选为v，求导简单者选为u。例如：∫Inx dx中应设U=Inx，V=x。

扩展资料：

分部积分法的实质：

1、将所求积分化为两个积分之差，积分容易者先积分。

2、实际上是两次积知巧分。

3、有理函数分为整式（即多项式）和分式（即两个多项式的商），分式分为真分式和假分式，而假分式经过多项式除法可以转化成一个整式和一个搭扰键真分式的和．可见问题转化为计算真分式的积分。

参考资料来源：百度百科-分部积分法