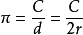祖冲之有关圆周率的故事是什么？

故事：一天早上，祖冲之正在家中读书，读的就是那刘徽做了注的《九章算术》，看到“割圆术”处，心想：将那正多边形的边数算到96个并不算多，多边形的周长与圆周长相差还甚远，为何不再多算一些。正多边形的边长愈多，多边形的周长不就更接近圆周长了吗？那算出的周率不就更精确了吗？想着想着，抬头一看，正见儿子在外玩耍，便叫道：“暅儿，你且去后山砍两根竹子来。”祖冲之的儿子叫祖暅，聪明伶俐，受祖冲之的影响，耳濡目染，也喜欢了数学，后来也成了数学家，提出了著名的“祖暅定理”。听见父亲唤自己，急忙跑了进来问道：“爹，唤儿有什么事情？”祖冲之说道：“你去后山砍一根毛竹来。”暅儿问道：“又要做算筹？”祖冲之答道：“不错，你去砍了与我拿来。”成就：祖冲之在数学上的杰出成就，是关于圆周率的计算。三国时期，刘徽提出了计算圆周率的科学方法——“割圆术”，用圆内接正多边形的周长来逼近圆周长。刘徽计算到圆内接96边形，求得π=3.14，并指出，内接正多边形的边数越多，所求得的π值越精确。祖冲之在前人成就的基础上，经过刻苦钻研，反复演算，求出π在3.1415926与3.1415927之间，并得出了π分数形式的近似值，取22/7为约率，取355/113为密率，其中六位小数是3.141929，它是分子分母在1000以内最接近π值的分数。