高数小问题df(x)和f(x)dx有什么区别？

1、含义不同：

df(x)是对f(x)求导。f(x)dx是f(x)的微分。

2、定义不同：

dF(x)就是lim[x→0](ΔF(x))，dx就是lim[x→0](Δx)。

dF(x)=f(x)dx，就是F(x)的微分等于 F(x)的导察冲数f(x)乘上x的微分。

,3、写法不同：

df(x)的最后结果没有dx，而f(x)dx有。

扩展资料

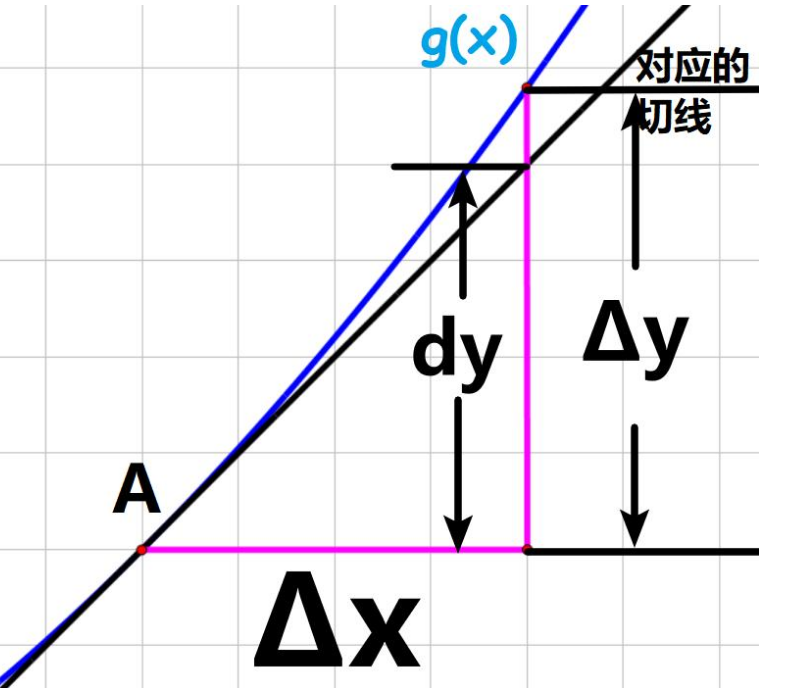
设函数y = f(x)在某区间内有定义，x0及x0+△x在这区间内，若函数的增量Δy = f(x0 + Δx) − f(x0)可表示为Δy = AΔx + o(Δx)，其中A是不依赖于△x的常数， o(Δx)是△x的高阶无穷小，则称函数y = f(x)在点x0是可微的。

AΔx叫做函数在点x0相应于自变量增量△x的微分，记作dy，即：dy=AΔx。微分dy是自变量改变量△x的线性函数，dy与△y的差是关于△x的高阶无穷小量，我们把dy称作△y的线性主部。

得出： 当△x→0时，△y≈dy。 导数的记号为：(dy)/(dx)=f′(X)，我们可以发现答轮，它不仅表示导数的记号，而且还可以表示两个微分的比值（把△x看成dx，即：定义自变量的增量等于自变量的微分），还可表示为dy=f′败举歼(X)dX。