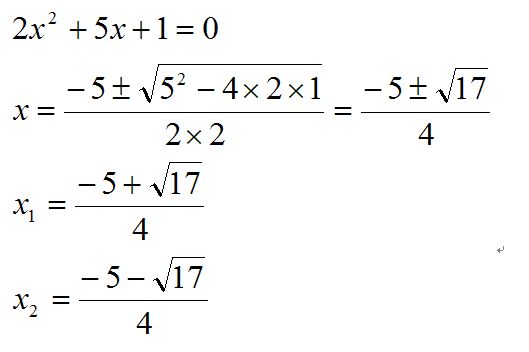X的平方等于8，X等于多少

x²=8；

x=±√8;

x=±2√2;

解题思路：根号算法

1、√ab=√a·√b﹙a≥0b≥0﹚ 这个可以交互使用.这个最多运用于化简，如：√8=√4·√2=2√2

2、√a／b=√a÷√b﹙a≥0b﹥0﹚

3、√a²=|a|（其实就是等肆棚丛于绝对值）这个知识点是二次根式重点也是难点。当a＞0时，√a²=a（等于它的本身）；当a=0时，√a²=0；当a＜0时，√a²=－a(等于它的相反数)

4、分母有理化：分母不能有二次根式或者不能含有二次根式。当分母中只有一个二次根式，那么利用分式性质，分子分母同时乘以相同的二次根式。如：分母是√3，那么分子分母同时乘以√3。

当分母中含有二次根式，利用平方差公式使分母有理化。具体方法，如：分母是√5 －2（表示√5与2的差）要使分母有理化，分子分母裂樱同时乘以√5＋2（表示√5与2的和）

扩展资料：

一元一次方程

只含有一个未知数，且未知数次数是一的整式方程叫一元一次方程（linear equation with one unknown）。通常形式是ax+b=0(a，b为常和氏数，且a≠0）。

一般解法

去分母 方程两边同时乘各分母的最小公倍数。

去括号 一般先去小括号，再去中括号，最后去大括号。但顺序有时可依据情况而定使计算简便。可根据乘法分配律。

移项 把方程中含有未知数的项移到方程的另一边，其余各项移到方程的另一边移项时别忘记了要变号。(一般都是这样：（比方）从 5x=4x+8 得到 5x - 4x=8 ；把未知数移到一起！

合并同类项 将原方程化为ax=b(a≠0)的形式。

化系数为一 方程两边同时除以未知数的系数。

得出方程的解。

例如：

3x=5×6

解：3x=30

x=30÷3

x=10

（注：解方程时最好把等号对齐）

参考资料来源：百度百科——方程