一、性质不同
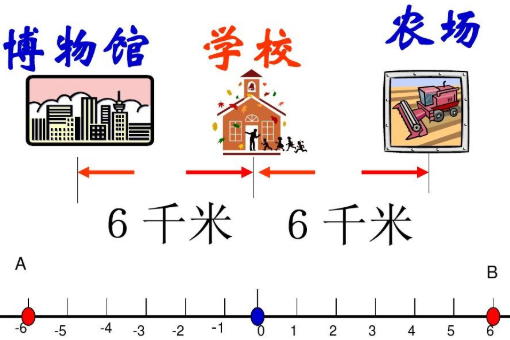
1、绝对值:一个数在数轴上所对应点到原点的距离。
2、相反数:绝对值相等,正负号相反的两个数互为相反数。
二、特性不同
1、绝对值特性:如果a.b相对,则a+b=0,反之亦然,如果a+b=0,则a和b相对。
2、相反数特性:绝对值或模数| x | 的非负值,而不考虑其符号,即| x | = x表示正x,| x | = -x表示负x(在这种情况下-x为正),| 0 | = 0。
三、代数意义不同
1、绝对值代数意义:在数轴上,从一个数到它的原点的距离称为那个数的绝对值。| a-b | 表示数轴上代表a和b的点之间的距离。
2、相反数代数意义:和为0的两个数相对,0的相反数还是0。
四、几何意义不同
1、绝对值几何意义:
(1)非负数的绝对值(正和零)本身,非正数(负数)的绝对值是相反的。
(2)实数A的绝对值总是一个非负数,也就是| a | ≧0。相互对立的两个数的绝对值是相等的,即| a |=| -a |(因为在数轴上它们到原点的距离相等)。
(3)如果a是正数,那么满足| x |=a的x有两个值±a,如| x |=3,则x=±3。
2、相反数几何意义:
(1)相对数的几何意义在数字的轴上,由两个点相等的距离表示的两个数与原点的两侧是相反的。
补充第1条:这对相反数一定为绝对值。
(2)在该数轴上,两个相对数的两点(除0)位于原点的两侧,相对于原点对称。
(3)此时,b的相反数为﹣b=﹣(﹣a)=a,所以说相反的数是对称的。
参考资料来源:
参考资料来源:
2.3相反数与绝对值教案
【知识回顾】
1.规定了_______、_______、_______的直线叫数轴.
2.有理数包括_______、_______、_______,数轴上的原点表示有理数_______,原点在左边的数表示_______.
3.数轴上到原点距离为2的点所表示得数是_______.
【教学目标】
1.借助数轴,理解相反数的意义,知道互为相反数的一对数在数轴上的位置关系;会求有理数的相反数。
2.借助数轴,理解绝对值的意义,知道︱a︱的含义(这里a表示有理数);会求一个数的绝对值;会利用绝对值比较两个负数的大小。
3.初步体会数学中的分类讨论思想.
【学习重点与难点】
重点:相反数和绝对值的定义
难点:绝对值的化简与计算
【学习过程】
导入新课
前面我们学习了有理数和数轴,通过本节课的学习,我们能进一步体会数轴在研究有理数中所起的重要作用.
学习新知
(一)相反数的意义及表示方法
1.自学要求:自主学习课本第23页至实验与探究前的内容,并解决以下问题:
①什么叫相反数;
②互为相反数的两个数在数轴上有什么特点;
③如何求相反数.
2.自学测试:
⑴分别写出下列各数的相反数
5_______-7_______ _______+11.2_______
⑵化简下列各数
①-(+10)=_______②+(-0.15)=_______
③+(+3)=_______④-(⑶回答下列问题:
1、绝对值:一个数在数轴上所对应点到原点的距离。
2、相反数:绝对值相等,正负号相反的两个数互为相反数。
相反数是只有符号不同的两个数互为相反数,在数轴上,位于原点的两侧,且与原点的距离相等的两个点所表示的数互为相反数
在数轴上,一个数所对应的点与原点的距离叫做这个数的绝对值,互为相反数的两个数的绝对值相等。
相反数,两个数之和为零,互为相反数,如2和-2,所以相反数可正可负;
绝对值,2的绝对值为2,-2的绝对值也是2,绝对值不会是负的。另外,绝对值其实是一个数到原点的距离,相反数是一个数。