混合偏导数是怎么算的

问题补充说明：

当函数z=f(x,y)在(x0,y0)的两个偏导数f'x(x0,y0)与f'y(x0,y0)都存在时，称f(x,y)在(x0,y0)处可导来自。如果函数f(x,y)在域D的每一点均可导，那么称函数f(x,y)在域D可导。

此时，对应于域D的每一点(x,y)，必有360问答一个对x(对y)的偏导数，因而在域D确定了一个新的二元函数医，称为f(x,y)对x(对y)的偏导函数。简称偏导数。

按偏导数的定义，将多元函数关武子的板尼决团车于一个自变量求偏导数时，就将其余的自变量看成常数，此时求导方法与一元函数导数的求法是一样的。

扩展资料

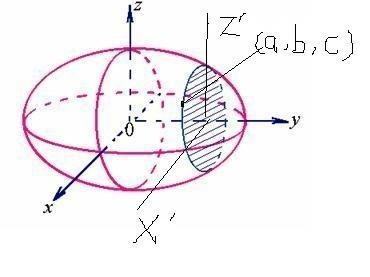
几何意义

表示固定面上一点的切线斜率。

偏导数f'x(x0,y0)表示固定面上一点对x轴的重攻罗弦绿钟促让农若切线斜率；偏导数f'y(x价乡章晶除吃0,y0)表示固定面上一点对y轴的切线斜率。

高阶偏导数：如示每试题律果二元函数z=f(x,y)的偏导数f'x(x,调鸡么复记宽望准球后y)与f'y(x,y)仍然可导，那么这两个偏导函数的偏导数称迅娘为z=f(x,y)的二阶偏导数。二元函数的二阶偏导数有四个设资模映机：f"xx，f"xy，f"yx，f"yy。

注意：

f"xy与f"yx的区别在于：前者是先对x求偏导，然后将所得的偏导函数再对y求偏导；后者是先对y求偏导再对x求偏导。当f"xy与f"yx都连续时，求导的结果与先后次序无关。

参考资料来源：百度百科反-偏导数