余弦定理怎么证明？

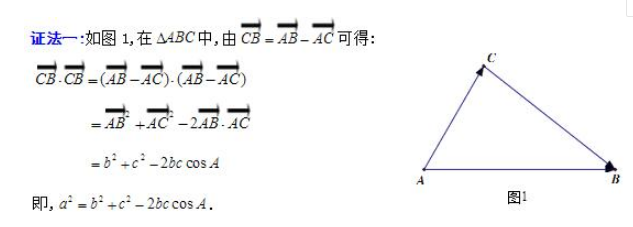
余弦定理，是描述三角形中三边长度与一个角的余弦值关系的数学定理，余弦定理是揭示三角形边角关系的重要定理，直改神接运用它可解决一类核高亏已知三角形两边及夹角求第三边或者是已知三个边求角的问题，若对余弦定理加以变形并适当移于其它知识，则使用起来更为方便、灵活。

余弦定理证明方法如图所示：

平面向量证法：

∵如图，有a+b=c(平行四边形定则：两个邻边之间的对角线代表两个邻边大小）。

∴c·c=(a+b)·(a+b)。

∴c²=a·a+2a·b+b·b∴c²=a²+b²+2|a||b|Cos(π-θ)。

（以上粗体字符表示念纳向量）。

又∵Cos(π-θ)=-Cosθ。

∴c²=a²+b²-2|a||b|Cosθ（注意：这里用到了三角函数公式）再拆开，得c²=a²+b²-2abcosC。

即cosC=(a2+b2-c2)/2*a*b。

同理可证其他，而下面的cosC=(c2-b2-a2)/2ab就是将cosC移到左边表示一下。