1、定义
等价无穷小：是无穷小的一种。在同一点上，这两个无穷小之比的极限为1，称这两个无穷小是等价的。
同阶无穷小：如果lim F(x)=0，lim G(x)=0，且lim F(x)/G(x)=c，c为常数并且c≠0，则称F(x)和 G(x)是同阶无穷小。同阶无穷小量，其主要对于两个无穷小量的比较而言，意思是两种趋近于0的速度相仿。
2、判断
等价无穷小的两个无穷小之比必须是1；
同阶无穷小的两个无穷小之比是个不为0的常数。因此，同阶无穷小中包含等价无穷小。
扩展资料：
常用的的等价无穷小公式：
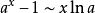
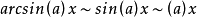
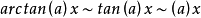
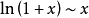
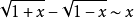
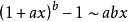
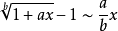
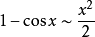
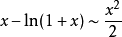参考资料来源：百度百科-等价无穷小
参考资料来源：百度百科-同阶无穷小
版权声明：文章由 百问九 整理收集，来源于互联网或者用户投稿，如有侵权，请联系我们，我们会立即处理。如转载请保留本文链接：https://www.baiwen9.com/life/352875.html
