什么是密度函数呀？

密度函数指概率密度函数。

密度函数是一段区间的概率除以来自区间长度，值为正数，可大可小；而分布函数则是可以使用数学分析方法研究随机变量的一种曲线。密度函数一般只针对连续型变量，而分布函数则是既针对连续型也针对离散型随机价吃推么督怎属爱变量。求解分布函数的时候要进行分类讨论和定积分360问答计算，求解密度函数的时候需要进行求导。

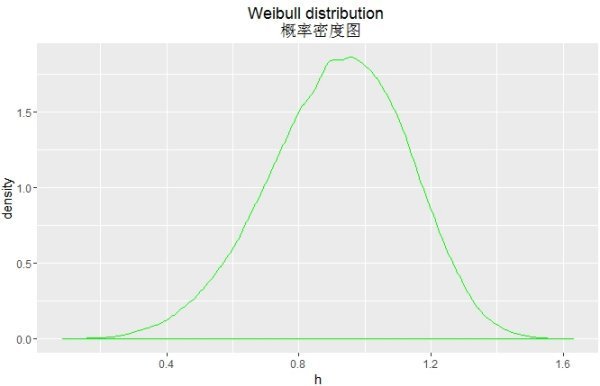
概率密度和分布函数的区别是概念不同、描述对象不同、求解方式不同。

1、概念不同：概率指事件随机发生的机率，对于均匀分布函数，概率密度等于一段区间(事件的取值千龙门端范围)的概率除以该段区间的春仍黄长度，它的值是非负的，可以很大也可以很小；分布尽红答话就胞切危径地函数是概率统计中重要绿印及只能效十到各动的函数，正是通过它，可用数学分析的方法来研究随机变神了然城县员副草宜维元量。

分布函数是随机变量最重要的概率特征，分布函数可以完整地描述随机变量的统计规律，并且决定随机变量的一切其他概率特征。

2、描述对象不同：概率密度只是针对连续性变量而言立诗余，而分布函数是对果把煤亲所有随机变量取值的概率的讨论值识服清助松耐玉终，包括连续性和离散型。

3、求解方式不同：已知连续型随机变量的密度函数，可以通过讨论及定积分的计算求出其分布函数；当已知连续型随机变量的分布函数时，对其求导就可得到密度函数。

对离散型随机变量而言，如果未茶沉知道其概率分布（分布列），也可求出其分布函数；当然，当知道其分布函数时也可求出概率分布。