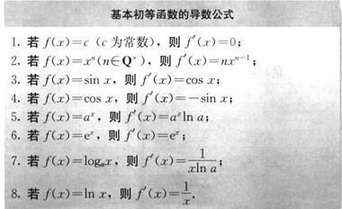1.y=c(c为常数) y'=0
2.y=x^n y'=nx^(n-1)
3.y=a^x y'=a^xlna
y=e^x y'=e^x
4.y=logax y'=logae/x
y=lnx y'=1/x
5.y=sinx y'=cosx
6.y=cosx y'=-sinx
7.y=tanx y'=1/cos^2x
8.y=cotx y'=-1/sin^2x
9.y=arcsinx y'=1/√1-x^2
10.y=arccosx y'=-1/√1-x^2
11.y=arctanx y'=1/1+x^2
12.y=arccotx y'=-1/1+x^2
a是一个常数,对数的真数,比如ln5 5就是真数
log对数 lognm 这里的n是指底数,m是指真数,当底数为10时,简写成lgm 当底数为e(e = 2.718281828459
是一个常数 数学中成如冲为超越数 经常要用到)时,简写成lnm
扩展资料:
如果函数f(x)在(a,b)中每一点处都可导,则称f(x)在(a,b)上可导,则可建立f(x)的导函数,简称导数,记为f'(x)
如果f(x)在(a,b)内可导,且在区间端点a处的右导数和端点b处的左导数都存在,则称f(x)在闭区间[a,b]上可导,f'(x)为区间[a,b]上的导函数,简称导数[1]。
若将一点扩展成函数f(x)在其定义域包含的某开区间I内每一个点,那么函数f(x)在开区间内可导,这时对于内每一个确定的值,都对应着f(x)的一个确定的导数,如此一来每一个导数就构成了一个新的函数,这个函数称作原函数f(x)的导函数,记作:y'或者f′(x)。
函数f(x)在它的每一个可导点x。处都对应着一个唯一确定的数值——导数值f′(x),这个对应关系给出了一个定义在f(x)全体可导点的集合上的新函数,称为函数f(x)的导函数,记为f′神世(x)。
参考资游橡肢料:百度百科-导函数